Notes on Absolute Value – Case 1

Absolute values do not have to be difficult to learn or work with.  In fact, they can be quite easy if you can understand what is happening instead of trying to memorize a bunch of complicated procedures.  In this first of four parts, let’s consider solving .

The first thing we need to understand is that the absolute value is telling us how far from zero the quantity it surrounds is.  In this case, it is telling us that  is exactly seven units from zero.  We can draw this on a number line.

<--+--O--+--+--+--+--+--O--+-->

     -7        0        7

So label the parts with what we know, namely that  is the part (red) that is exactly seven units from zero.

<--+--O--+--+--+--+--+--O-+-->

     -7        0        7

So now we have to solve the two equations.

Now we just draw what the equations are telling us to draw.

<--+--O--+--+--+--+--+--O-+-->

     -1     0           6

Notice that the resulting graph looks identical to the original graph except for the labeling of the scale.  This will always be true!

Notes on Absolute Value – Case 2

Absolute values do not have to be difficult to learn or work with.  In fact, they can be quite easy if you can understand what is happening instead of trying to memorize a bunch of complicated procedures.  In this second of four parts, let’s consider solving .

The first thing we need to understand is that the absolute value is telling us how far from zero the quantity it surrounds is.  In this case, it is telling us that  is strictly less than seven units from zero.  We can draw this on a number line.

<--+--(--+--+--+--+--+--)--+-->

     -7        0        7

So label the parts with what we know, namely that  is the part (red) that is less than seven units from zero.

<--+--(--+--+--+--+--+--)--+-->

     -7        0        7

     -7  <     <   7

After all, inequalities always point to the left on the number line!  So now we have to solve the compound inequality.

Now we just draw what the inequality is telling us to draw.

     -1   <    x    <   6

<--+--(--+--+--+--+--+--)--+-->

     -1     0           6

Notice that the resulting graph looks identical to the original graph except for the labeling of the scale.  This will always be true!

Notes on Absolute Value – Case 3

Absolute values do not have to be difficult to learn or work with.  In fact, they can be quite easy if you can understand what is happening instead of trying to memorize a bunch of complicated procedures.  In this third of four parts, let’s consider solving .

The first thing we need to understand is that the absolute value is telling us how far from zero the quantity it surrounds is.  In this case, it is telling us that  is strictly more than seven units from zero.  We can draw this on a number line.

<--+--)--+--+--+--+--+--(--+-->

     -7        0        7

So label the parts with what we know, namely that  is the part (red) that is more than seven units from zero.

<--+--+--)--+--+--+--+--+--(--+-->

        -7        0        7

 < -7       OR        7 <

After all, inequalities always point to the left on the number line!  So now we have to solve the compound inequality.

Now we just draw what the inequality is telling us to draw.

    x < -1       OR        6 < x

<--+--+--)--+--+--+--+--+--(--+-->

        -1     0           6

Notice that the resulting graph looks identical to the original graph except for the labeling of the scale.  This will always be true!

Notes on Absolute Value – Case 4

Absolute values do not have to be difficult to learn or work with.  In fact, they can be quite easy if you can understand what is happening instead of trying to memorize a bunch of complicated procedures.  In this last of four parts, let’s consider solving .

The first thing we need to understand is that the absolute value is telling us how far from zero the quantity it surrounds is.  In this case, it is telling us that  is exactly as far from zero as is.  What are the possibilities?

It turns out that there are only two possibilities – either they are both on the same side of zero, in which case they must be the same number, or they are on opposites sides of zero, in which case one must be the opposite of the other.  Therefore, we write two equations and solve both.

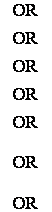
This marks the end of our discussion on Absolute Value.