A Note on Factoring

Consider the trinomial  and let’s use both methods for factoring it.

First, look at the “ac” or “grouping” method for factoring.  This method gets its name from the fact that we have defined the standard form for a general quadratic trinomial to be  and we will be using the leading coefficient and constant term to create a product to factor; then we will use those factors to create a polynomial we can factor by grouping.  For the trinomial above,  so we need to list the factors of .

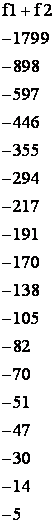
I have listed the sum of the factors in each case because what we are seeking is the pair of factors that add to give us  in the trinomial we are attempting to factor.  In this case, we have  so the pair of factors that we want is  and .

Since , we can substitute in our original trinomial as follows:

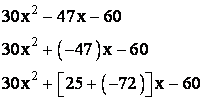
Applying the Distributive Property, we now have

Now we want to factor this four-term expression by grouping the terms 2 and 2 like this:

For emphasis, I want to rewrite this using only addition.

Now, factor the Greatest Common Factor from each pair.

Noting that  is common to both of these terms, we now factor it out.

Simplifying, we obtain our final result.

There are several things to point out about what we have done which can aid us in doing this kind of problem:

1)  We could have written  instead of .  In that case, our steps would have remained the same, but each would have “looked” slightly different.  Our final result would have been  which is equivalent to what we have above because of the Commutative Property of Multiplication.

2)  Although we initially listed all 36 possible factors for , we could have cut that number in half by noting that  implies that the factor with the larger absolute value must be the one that is negative.

3)  If the product  ac  is positive, there will still be two cases for each pair of factors – one case will have both factors positive and the other case will have both factors negative.  Again, we can use the sign on b to cut the number of pairs we have to consider in half.

4)  A major advantage of this method, although there is still some trial and error involved, is that we can use the same method both for the case where the leading coefficient is 1 and where the leading coefficient is not 1.  Here is a quick example of how it would work when the leading coefficient is 1:

[Note that  when the leading coefficient is 1.]

Consider the trinomial

Since , we proceed as follows:

I leave it to you to supply the reasons for each step.

Now let’s return to our original trinomial  and look at what is involved if we are to use strictly trial and error.

The factors of  are                           The factors of    are

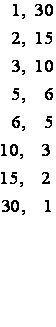
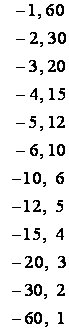
[Note:  It is not necessary to consider the case where both factors of  are negative since we can simply factor  out of both factors and reduce it to the case where both factors of  are positive.]

Since we must consider all possible pairings, there will be  separate cases to be listed and checked.  (Checking is by multiplying out the proposed factors!)  To get the idea, I will list only the first several cases.

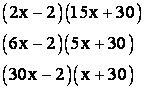
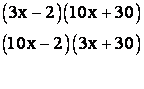
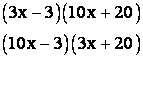
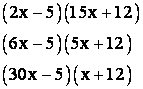
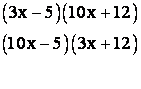
and so on until all 96 cases are listed!  There have been a number of techniques developed over the years to try to make this process more efficient, but each requires that a significant amount of the work be done in your head to avoid so much writing.  None of these trial and error techniques is very satisfactory when compared with the efficiency of the “ac” or “grouping” method.