Long Division of Polynomials

The main thing to keep in mind when dividing is that we are patterning our procedure after the one we use for long division of numbers.  Let’s look at that for a moment.

We start by asking how many times 11 will go into 14.  After deciding 1 is the answer to this part, we have:

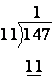
Then we subtract 11 from 14 and bring down the 7.

Okay, so now we find 11 goes into 37 only 3 times and have.

Last, we subtract 33 from 37 to get a reminder of 4.

For a moment, let us take a look at the Division Algorithm because we frequently will use a modified form of it to write our result.

Long Division: 

Division Algorithm: 

This may look familiar because this is the way most of us were taught to check our work when dividing.  We obtain a modified form by dividing every term in the Division Algorithm by the divisor.

This also may look familiar because it is the form we use to write an improper fraction in mixed number form.  Our example would become  and we would finally write the result as .

Okay, now let’s look at a polynomial problem.

We ask how many times x will go into 5x² and get 5x.

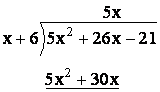
Now, we subtract, just the way we did with numbers, so 5x² from 5x² gives 0 and 30x from 26x requires us to think in terms of signed numbers, like this

So what we have looks like this after we bring down the constant term.

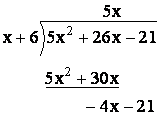
How many times will x go into –4x?  Well, we get –4.  So now we have this.

When we subtract, we get 3 and that yields the result.

Note that we once again were dealing with signed numbers in the final subtraction .

If we were to use the modified form of the Division Algorithm here we would obtain the following result:

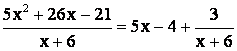
Now, let’s look more closely at just the first subtraction.  Some people do not like doing it as subtraction, so what they do is move over to the side, distribute the minus sign (for subtraction) through what is being subtracted, and then add the resulting polynomials.  It might look like this.

 becomes

Whether we subtract on the left or add on the right, we will get the same result because subtracting a quantity is the same as adding its opposite.