Notes on Solving Rational Equations

There is frequently more than one way to approach a problem.  Here is an example of an alternate approach to solving equations involving rational expressions and determining whether or not a solution might be extraneous.

Recall that the domain of an expression is the set of all real numbers that can be substituted in place of the variable.  We can use this concept to advantage when solving equations involving rational expressions.  In fact, we find that a little effort at the beginning can save us quite a bit of time and effort at the end.

What we want to do is examine the expressions in the equation and determine the domain of each.  Then we intersect the separate domains to arrive at the domain of the whole equation.  If we have done this properly, when we get to the point that we have possible solutions to check, it is only necessary to check each solution to make sure it is in the domain of the equation.  Anything in the domain of the equation is acceptable; anything else is unacceptable.

Perhaps it would be a good idea to look at an example of how to do this.

Consider .

For the first expression, , the domain is .

For the second expression, , the domain is .

For the third expression, , the domain is

The intersection of these sets is .

So what we know now is that neither 0 nor 3 can be a solution to this equation.

To solve the equation, our first step is to multiply both sides of the equation by the Lowest Common Denominator and then simplify the resulting expressions as much as possible.

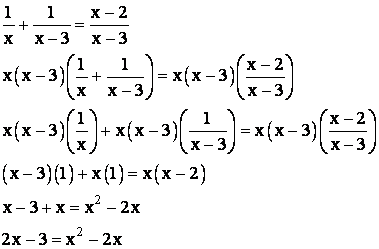
At this point, we recognize that we have a quadratic equation to solve, so we get everything on one side of the equal sign, simplify everything, and factor the resulting polynomial.

Now, we can apply the Zero Factor Property to solve for x.

When we examine the domain for the equation, we find that it includes 1 but it does not include 3.  Therefore, 3 is extraneous and 1 is the only solution.

This type of problem allows us to see a definite difference between foresight and hindsight in solving problems.  Foresight is better, but it requires more thought.