Introduction
Before we begin to explore the transcendental functions, I will list here the results with which I will be assuming everyone is familiar. Of course, a basic knowledge of the Differential Calculus is assumed in addition to the specific items listed here. We will follow the more modern approach to the development of the necessary concepts in this series of notes and present the classical approach later.
The number e. There are two common definitions for e in use in College Algebra courses today. Although they are described with words there, we can use limit notation here to state them:
and 
It is relatively easy to see
that the two are equivalent if we let 
. When needed, we will use
which ever form is the most appropriate at the time.
One way to see how interest in these limits came about is to consider the formula for compound interest. Let B represent the balance in the account after t years at an annual interest rate of r with n compounding periods in one year, where P is the initial amount invested in the account. The formula is then written:
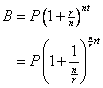
Now, letting 
, we
have 
and
we can see that n and k are directly proportional for a fixed
interest rate.
Exponential functions. We extend the definition of exponent using the
concept of limit by first noting that for any Real Number, there is a sequence
of rational numbers that converges to it. To be exact, let r represent
any real number. There is a sequence of Rational Numbers, say 
, such
that 
.
We then proceed with the following definition: For any Real Number 
,
define 
. This permits us to
define a function, which we call an exponential
function, as 
, for all Real Numbers x
and b a positive Real Number. We generally exclude 
from
consideration here because it reduces simply to the constant function 
.
Logarithm functions. For simplicity, we define the logarithm functions
through a notational equivalence – 
is equivalent to 
, where b
is a positive Real Number different from 1, y is any Real Number, and x
is necessarily a positive Real Number. We make two additional Notational
conventions:
, which is called the
common logarithm and
, which is called the
natural logarithm.
Basic properties of logarithms. There are three basic properties of logarithms that will be used frequently:
,
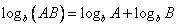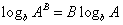, and
.
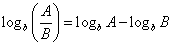Inverse function. We define a function g to be the inverse of
a function f and denote it by 
if two conditions hold:
for all x in the
domain of and
for all x in the
domain of f.
Note that, in general, 
.
Relation between
exponential and logarithm functions.
From the definition of logarithm functions, we can substitute in the first
equation for x from the second equation and have 
. We can
substitute in the second equation for y from the first equation and have
.
In conjunction, these two statements tell us that, for a given base, the
exponential function and the logarithm function are inverses.
Change of base formula. We will occasionally have need of the ability to change logarithms from one base to another. Let us assume that b is the base of the given logarithmic expression and c is the base of the logarithm with which we desire to work. We can derive a useful formula for changing the base of the logarithm as follows.
Let 
and write the
equivalent exponential equation – . Now, evaluate the both
sides of the equation with the logarithm function base c. and use the
properties of logarithms to solve for y.
Therefore, we have what is
commonly referred to as the change of base formula,
namely 
. Our most frequent
application will be to change to base e, so we will most often see it as
.