Derivatives of Inverse Functions

What we wish to examine here is the procedure we used to obtain the derivative of the Natural Logarithm function.  In effort to keep the notation from getting in the way, we will let  represent a known function with a derivative we already know and  will represent the inverse function.  Our goal is to obtain the derivative of the latter function.  In particular, we have .  We will differentiate the resulting equation  and solve it for .  (Note the application of the Chain Rule.)

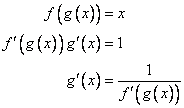
This rather simple result will actually permit us to find derivatives of some functions that it would be very difficult to differentiate directly.  We have already seen this when we found the derivative of the Natural Logarithm function.

We can verify that what we have done is correct by applying it to a function for which we already know the derivative of its inverse.  Let  and .  We already know that  and .  Let’s put this into our formula and verify that we get the same result.

In a later note, we will apply this formula to a whole class of functions to find derivatives that might be surprising in some cases.