The Inverse Hyperbolic Functions

Let us derive the inverse of the hyperbolic sine function, , by first letting  and then solving for  in terms of .

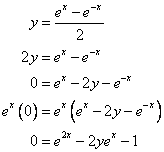
We can use the Quadratic Formula to solve this quadratic-like equation and continue to solve for x in terms of y as follows.

Noting that  and , we conclude that  and find that .  This gives us the desired result.

The other inverse functions are listed below.

You may attempt to derive these formulae in a manner similar to the one above or you may simply verify that the definition of an inverse function is satisfied by each of the above formulae.  Either way, you should become familiar with these formulae.

You should also verify the following differentiation formulae for the inverse hyperbolic functions.