Logarithmic Differentiation

In addition to the other uses you have seen for the Natural Logarithm function, we are now in a position to discuss an application of it in Calculus that can save a lot of time and effort.  In addition, it will allow us to differentiate some functions that we might otherwise find very difficult to differentiate.  This application is called Logarithmic Differentiation and it relies on the properties of the Natural Logarithm function and Implicit Differentiation for its power.

The basic idea can be shown with some relatively simple functions.  For example, let’s consider .  Easily written, this function does not appear to be easily differentiated.  However, if we replace  with  and apply the Natural Logarithm function to both sides of the equation, look at what happens.

Now we can differentiate both sides of this equation and solve the result for .

In the last step, we simply returned to the function notation to show that we have the derivative of our original function.

Let’s look at another type of example where we will definitely see a time and work saving.  Consider 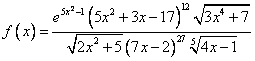.  Okay.  Yes we could do this directly using in combination the product rule, the quotient rule, and the chain rule multiple times.  This would require a lot of work, time and paper and would be subject to many possible errors.  Watch what happens when we apply the above procedure to this function.

Now we are ready to differentiate.

Granted that it will be some work to get this to simplest form, but the really hard work has been done!

Keep your eyes and mind open as you approach problems and you will begin to see places where this technique can be applied to make some problems much easier.